User:Dg
SoC2009 Dev Ghosh
Abstract
Hugin creates wide-angle photo panoramas taken from a single camera position, one of the most popular applications of stitching software. However, when viewing a flat object such as a painting, photographs taken from different, casually chosen viewpoints must be combined to create a large high-resolution image mosaic. But Hugin can’t assemble photo mosaics of large flat objects photographed from many different camera locations. While tweaking Hugin’s settings can provide an approximate result, the underlying Panotools imaging model does not include a projective homography integrated with lens distortion correction. The optimize-able imaging parameters are unable to fully rectify and align the tiles of a mosaic image. This results in mosaics with warped edges and significant distortions. The process requires awkward user interactions as shown in [1], a tutorial by Joachim Fenkes titled “Creating linear panoramas with Hugin.” Fenkes uses horizontal image features such as utility boxes aligned at the same height along the graffiti covered wall to straighten the snaking panorama. I propose to add a new “mosaic mode” to Panotools. This will introduce a new image model based on multiple centers of projection to generate high-resolution, distortion-free images of flat objects captured with either handheld or tripod-mounted cameras.
[1] http://www.dojoe.net/tutorials/linear-pano/
Details
Problem
Users of Hugin have developed methods for stitching 2D scanned objects and stitching linear panoramas. For best results, these methods rely on matching line constraints (control points of type horizontal or vertical line). But on images lacking clear horizontal or vertical features, when only manually placed or SIFT-generated control points are available, such approaches result in poorly aligned mosaics.
Solution
The Panotools imaging model optimizes eight parameters to correct lens distortion and geometric alignment. However, this model is unable to describe warps between overlapping images of a planar object taken from different viewpoints. While leaving the existing lens distortion parameters in place, I propose to develop an extended geometric model describing the relationship between a orthographic view of a planar object with a perspective view of a subsection of the object. This model will be optimized using the existing Levenberg-Marquardt optimizer. The optimized parameters will allow us to project each view of a subsection of the object as if it were viewed with a large, high-resolution, orthographic camera or with a perspective camera from a distance sufficient to view the whole. This approach will also allow views of the object taken from low angles to be projected and mapped to the orthographic view.
Performance Measures
The new geometric model will be tested on synthetic image data and overlapping views of a large painting in the collections at the Art Institute of Chicago. The results will be compared to those obtained using Panotools’s current model by average and worst control point distance and by image differencing in overlap regions.
Project Timeline
I plan to spend at least 40 hours a week dedicated to this project. I have already begun to explore and make modifications to the source code. This head start will allow me to work through the months of April and May and continue through the end of Summer of Code. These are the steps I plan to take:
• Study current model for projection of images in libpano13 (prior to May 23)
• Research existing models for viewing images photographed from different viewpoints including “Gold Standard” Direct Linear Transform algorithm and Szeliski’s Image Alignment and Stitching: A Tutorial (prior to May 23)
• Develop geometric model for viewing of mosaic (two weeks)
• Implement new model in Panotools (five weeks)
• Test model on synthetic and real image data sets (two weeks)
• Evaluate performance by comparing alignment attempts with existing model (in average control point error) (two weeks)
• Wrap up and complete documentation (one week)
Deliverables
• Documentation describing geometric model
• A library implementing the model
• Results of tests of library
• Fully-commented source code
Biography
I have been experimenting with Hugin since Summer 2008 and started to build my own version and modify the source code in December 2008. I built Hugin both on Windows and on Linux under Ubuntu. My interest is in using Hugin to assemble large, high-resolution mosaics of paintings photographed from different viewpoints with 50% or more overlap.
I am a PhD candidate in Electrical Engineering and Computer Science at Northwestern University, Evanston, Illinois. I have coding experience in Python, C/C++, and MATLAB. My background is in video, signal, and image processing and my previous projects have included making improvements to the Joint Scalable Video Model, a scalable version of the H.264 video codec written in C++. I enjoy taking pictures and solving problems and participating in Google’s Summer of Code will allow me to work solely on this project over the summer without other distractions.
References
• http://hugin.sourceforge.net/tutorials/scans/en.shtml
• http://www.dojoe.net/tutorials/linear-pano/
• Zhang, Z. and He, L.-W. (2007). Whiteboard scanning and image enhancement. Digital Signal Processing, 17(2), 414–432.
• http://www.ics.forth.gr/~lourakis/homest/
• http://grail.cs.washington.edu/projects/multipano/
• Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in computer vision. Cambridge University Press.
• Richard Szeliski (2006) Image alignment and stitching: a tutorial. Now Publishers Inc.
- End of Proposal
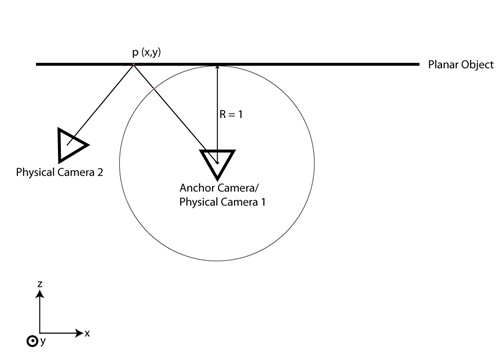
Week 1: Initial Approach
Below, we see a top view of the planar object we wish to image. The circle represents the panosphere and the triangles represent the viewing frusta of two cameras. We wish to project points on the planar object, p(x,y), as viewed from Physical Camera 2 to a virtual (output) Anchor Camera, coincident with Physical Camera 1.
To do this, we propose to add a position for each image (x,y,z). All images with non-zero (x,y,z) coordinates are projected to the plane. The location of the plane will be described by the yaw and pitch of a normal to the planar surface. (Note that Physical Camera 1/Anchor Camera is not necessarily perpendicular to the planar surface but it is located at (0,0,0) and is assumed to be 1 distance unit from the plane.)
Creating the output image takes two steps:
- We must map from the Anchor Camera onto the plane. This gives us a relation between angles on the panosphere and pixels on the plane .
- We must map from the plane to Physical Camera 2. This gives us a relation between pixels on the plane and the position of Physical Camera 2.
Next, the additional parameters added will be optimized. It is unknown whether this optimization will be successful or stable at this point.
Week 2: Understanding Panotools
This week, I've been going through filter.h and adjust.c, the two files that contain much of the code to setup transformations. I have added extensive comments to note my understanding of the code and uploaded the results to my branch. Between this detailed reading and review of some older communication on the hugin-ptx list,
http://groups.google.com/group/hugin-ptx/browse_thread/thread/c01fb82c91c7e502/d88a617e1860b691
I feel I have a much better understanding of the current model in panotools. I am working on a list of questions I plan to send to the mailing list over the weekend. Hopefully the answers will clear up the points that I'm still confused on.
From my talk with Daniel this week, I realized my most immediate task is to nail down which additional parameters will describe views captured from non-overhead viewpoints best. While Pablo's suggestion of having an x,y,z coordinate for each image is possible, I have been considering alternate descriptions such as the tilt and slant and distance of an image from a non-overhead view. I need to decide how to precisely define these parameters and which set will best model our system.
Week 3: MATLAB Modelling
This past week, I have started developing and testing my geometric model for remapping in MATLAB. Specifically, I have described the position of the plane with the parameters LookAtPoint, tilt, slant, and spin as follows:
- LookAtPoint is the point where a ray exiting the camera's center of projection intersects the image plane.
- tilt is a rotation about the x-axis centered at the LookAtPoint.
- slant is a rotation about the y-axis centered at the LookAtPoint.
- spin is a rotation about the LookAtPoint.
Because the image plane is located some distance from the center of projection, it's not easy to rotate about the x- or y-axis while centered at the LookAtPoint. So to implement the slant and tilt with straightforward matrix transformations, I have described them as a series of rotations and translations of the image plane.
The next step is to test if this series of transformations effectively causes images taken from what I called "Physical Camera 2" in the diagram[1] to appear as if they are viewed from the "Anchor Camera". I have a checkerboard surface that I plan to use as a sample planar object. MATLAB has image transformation functions that will allow me to easily test and view the effects of the image transformations I develop.
I plan to create diagrams illustrating this approach, but they are quite time-consuming to draw in Illustrator, so at the moment, my time is best spent coding and going off of hand-drawn sketches.
Week 4: Results of MATLAB Model
I've been testing a model in MATLAB for straightening slanted or tilted images. I have parameterized these geometric transformations as angular rotations about the y-axis for slant and x-axis for tilt.
As the attached document shows, simple matrix transformations straighten the slanted image plane so it lies parallel to the x-y plane. As the MATLAB code uploaded to my branch shows, this process is reversible when run on a set of points forming the corners of a square (and its center). The recovered points are exactly equal to the original points. (See Figure 1, if you run the mosaic_v11.m script)
I will continue with these tests, exploring how capable this approach is when correcting combinations of slants and tilts. Next I will conduct further tests on images. If successful, I will begin to place function prototypes for these transformations in my branch with the intermediate goal of creating the functions necessary to slant a panorama in Panotools by adjusting a command line parameter.