Difference between revisions of "Stitching a photo-mosaic"
Dgjohnston (talk | contribs) m |
|||
| Line 9: | Line 9: | ||
The typical case of a photo-mosaic is the [[linear panorama]], where one large subject like a wall, is photographed by taking photos of the wall, each covering a proportion of the wall, and moving the camera parallel to the wall with each shot. | The typical case of a photo-mosaic is the [[linear panorama]], where one large subject like a wall, is photographed by taking photos of the wall, each covering a proportion of the wall, and moving the camera parallel to the wall with each shot. | ||
| − | The classical way to stitch these kinds of mosaics was to lay the prints out on a light-table and glue them together. Now with the mosaic-mode in the panotools lens model, it is possible to use the software estimate the camera position including angles, lens distortion etc. and to re-project and stitch the images to a photo-mosaic. | + | The classical way to stitch these kinds of mosaics was to lay the prints out on a light-table and glue them together. Now with the mosaic-mode in the panotools lens model, it is possible to use the software to estimate the camera position including angles, lens distortion etc. and to re-project and stitch the images to a photo-mosaic. |
| Line 16: | Line 16: | ||
=== Parameters === | === Parameters === | ||
| − | The panotools [[Lens correction model|lens model]] has been expanded with addition of five new parameters that describe the camera position in [http://en.wikipedia.org/wiki/Cartesian_coordinate_system cartesian coordinates], TrX, TrY, and TrZ, and the yaw and pitch of the translation remapping plane, Tpy and Tpp. | + | The panotools [[Lens correction model|lens model]] has been expanded with the addition of five new parameters that describe the camera position in [http://en.wikipedia.org/wiki/Cartesian_coordinate_system cartesian coordinates], TrX, TrY, and TrZ, and the yaw and pitch of the translation remapping plane, Tpy and Tpp. |
| − | The [[yaw]], [[pitch]] and [[roll]] angles now apply | + | The [[yaw]], [[pitch]] and [[roll]] angles now apply to the camera around the camera's TrX, TrY and TrZ position in space. Together these six parameters describe where the camera viewpoint is (TrX,TrY,TrZ) and the direction the camera's optical axis point (y,p,r). |
=== Mosaic lens model === | === Mosaic lens model === | ||
In order to generate a photo-mosaic from the individual images, the panotools lens model re-projects the images in the following way. | In order to generate a photo-mosaic from the individual images, the panotools lens model re-projects the images in the following way. | ||
| − | * Each image is projected onto a plane with yaw Tpy and pitch Tpp (the translation remapping plane). This re-projection | + | * Each image is projected onto a plane with yaw Tpy and pitch Tpp (the translation remapping plane). This re-projection uses all the lens model's parameters; the position parameters described above, as well as FOV, distortion. etc. |
| − | * The plane is projected onto the panosphere | + | * The plane is projected onto the panosphere. |
| − | * The panorama camera, which gives the viewpoint of the photo mosaic, sits in the center of the panosphere and looks straight ahead at the panosphere (and the perpendicular projection plane). This camera gives the FOV of the whole photo-mosaic | + | * The panorama camera, which gives the viewpoint of the photo mosaic, sits in the center of the panosphere and looks straight ahead at the panosphere (and the perpendicular projection plane). This camera gives the FOV of the whole photo-mosaic. |
Revision as of 00:57, 3 February 2014
This section is a stub.
Definition of photo-mosaic
A photo-mosaic is an image that is stitched together by photographs all taken from different viewpoints. This differs from the panorama where all images are taken from one single viewpoint but with different angles.
The typical case of a photo-mosaic is the linear panorama, where one large subject like a wall, is photographed by taking photos of the wall, each covering a proportion of the wall, and moving the camera parallel to the wall with each shot.
The classical way to stitch these kinds of mosaics was to lay the prints out on a light-table and glue them together. Now with the mosaic-mode in the panotools lens model, it is possible to use the software to estimate the camera position including angles, lens distortion etc. and to re-project and stitch the images to a photo-mosaic.
Understanding the mosaic lens model
Parameters
The panotools lens model has been expanded with the addition of five new parameters that describe the camera position in cartesian coordinates, TrX, TrY, and TrZ, and the yaw and pitch of the translation remapping plane, Tpy and Tpp.
The yaw, pitch and roll angles now apply to the camera around the camera's TrX, TrY and TrZ position in space. Together these six parameters describe where the camera viewpoint is (TrX,TrY,TrZ) and the direction the camera's optical axis point (y,p,r).
Mosaic lens model
In order to generate a photo-mosaic from the individual images, the panotools lens model re-projects the images in the following way.
- Each image is projected onto a plane with yaw Tpy and pitch Tpp (the translation remapping plane). This re-projection uses all the lens model's parameters; the position parameters described above, as well as FOV, distortion. etc.
- The plane is projected onto the panosphere.
- The panorama camera, which gives the viewpoint of the photo mosaic, sits in the center of the panosphere and looks straight ahead at the panosphere (and the perpendicular projection plane). This camera gives the FOV of the whole photo-mosaic.
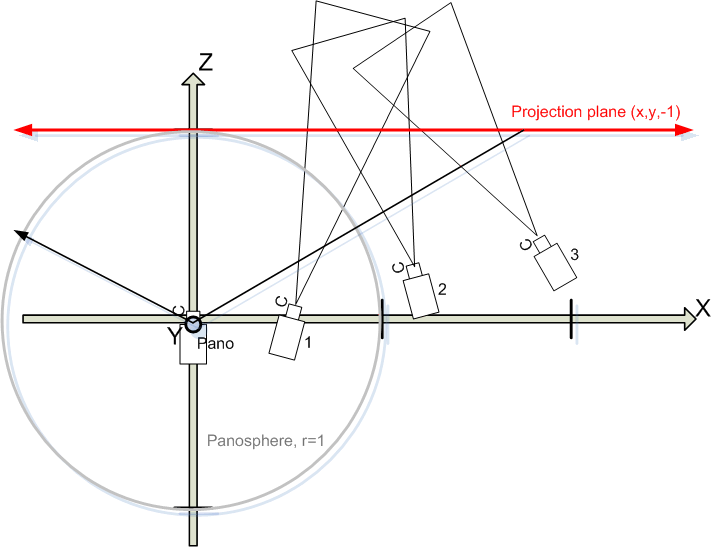
To illustrate the model, consider the following picture, which looks straight down at a photo mosaic which consists of three images taken "to the right" of the center.
- The unit-panosphere is drawn in gray.
- "The panorama camera" is centered in Origin, X,Y,Z =0. The translation remapping plane has default position Tpy=0 and Tpp=0.
- Three photos are taken with camera positions 1, 2 and 3 by varying TrX,TrZ and Yaw
- The photos are reprojected to a plane (red) that touches the panosphere in (0,0,1) and then onto the panosphere using the "Panorama camera"
Result
Because the projection plane is a plane and perpendicular to the panorama camera, there will be miss-fit when this assumption is not true for the real-world subject. For example, photos of a flat wall mural could be rendered perfect, while a three dimensional subject would not be.